How do you choose your dice for Dungeons and Dragons games?
Type of Dices in Dungeons and Dragons
Since 1974, Dungeons and Dragons, and many other Role Playing and other games since then, adopted a set of 5 dice. These included:
- 4 sided die (1d4)
- 6 sided die (1d6)
- 8 sided die (1d8)
- 12 sided die (1d12)
- 20 sided die (1d20)
The game uses the various dice to spice the play role gaming with varying randomness.
For example, a simple dagger generates 1d4 of damages, to know whether you hit your adversary, you use a 1d20 (with modifiers from their armor and your strength or dexterity), etc.
The 10 sided die (1d10) was introduce in 1980, 6 years after the very first Dungeons and Dragon box set. The die was presented at GenCon and it was said that it was invented around that time, which it was not...
What makes a die a good D&D die?
In my experience, the following points are what makes a die a good die.
But first, I wanted to mention that I have used these Random Polyhedral Wiz Dice (link to Amazon.com) which give you many 7-die sets1. These 100 dice have been enough for me, the Dungeons Master, and my five players. The only time more dice would be nice is when we all generate characters at the same time. Otherwise, you really get enough for a great game. (See the How Many Dice Are Needed for Dungeons & Dragons? section below)
Somehow, the most horrible dice I ever got where those that came in the Dungeons & Dragons box I got when I was 11. These were too light, the weight was not correctly balanced, the shapes were not so good either (some were warped).

Die Heavy Enough
A die needs to be heavy enough to roll well. In most cases, plastic dice do very well (although some plastics are just too light). Now if you want to go really heavy, you can get metallic dice such as these old looking copper dice you can find on Amazon.com.
As shown in the previous section, I first had really light dice that would not really roll at all... (these dice came with my very first Dungeons and Dragons box set. So yes... dice created by TSR, Gary Gygax and his cohort.)
Die Well Carved
A die is considered to be well carved when the weight removed by carving each number on a each side balances with the carving on the other sides. This is actually why the numbers are in the order they are and not to change the odds or something magical like that... you want a 1d20 to roll any one number about 5% of the time (see the statistics below.)
Die Internal Perfection
The die can't have an internal malformation. A plastic die that has a bubble inside will have a weight problem and thus certain numbers will come up more often—the bubble will tend to stay around the top because gravity pulls the heavier side down.
Note that most dice are made of plastic. It is possible to get wood and metallic dice too! I do not recommend wood as it tends to get chipped and in most cases makes for dice that are too light.
You often get wood dice in other games, not so much for Dungeons & Dragons.
Die Easy to Read
I think that there is nothing worst than a die you cannot read from the Master's position. Not that all gamers are cheaters, but often you go by another thought and need the number again and want to check it out again... and if you cannot read it, you have to ask the player slowing things down.
I recommend that you avoid dice with fancy numbers, or decorations on each face. These are really cute, but it makes it difficult to use in a smooth game.
The color contrast can be problematic too. This is not always easy to see when you just check out a picture if you buy your dice online. If you are looking at your very first set, a dark color with white digits will work best. I've also seen light color dice with black digits. These are a bit less common.
How Many Dice Are Needed for Dungeons & Dragons?
Now a day, one D&D die set is composed of seven dice.
- 1d4
- 1d6
- 1d8
- 1d10 (units)
- 1d10 (tenth)
- 1d12
- 1d20
This is the minimum one game of Dungeons & Dragons requires to make the game possible.
However, it's often necessary to roll multiple dices of a certain type at a time. For example, to create your character, you roll for his skills. This uses 3d6 or 4d6, depending on the method selected. Therefore, having at least four 6-sided dice is a must for that time.
Later, Wizards and others will roll many d6 as they roll fireball damages and if you have Magic Missiles, you will roll 4d4 each time.
In combat, you often have to roll 2d20. This happens when you have to roll with advantage or disadvantage.
So, in effect, having just one set is going to be difficult to play a whole game. What often happens, though, is that each player will have his own set. That way, with 3 to 5 players and the Dungeon Master, you can get about 6 sets which is good.
Another solution, is to get a large bag with many dice as I mentioned earlier, as such, a bag of 100 Random Polyhedral Wiz Dice will do magic for you!
What are the odds of each die? (statistics)2
Whenever you role a die, assuming it is well weighted, the odd of rolling a certain number is the inverse of the number of sides. So 1 divided by 12 for a d12 die, or about 8.3% chance of rolling a specific number. This was found by Galileo and Girolamo Gardano around 1600 AD, both of whom discovered statistics.
In many cases, you are asked to roll two or more dice. In that case, the total is likely to be closer to the middle number. So if you have to roll 4d6, the middle is 3.5 so your total is likely going to be close to 14:
(6 + 1) / 2 × 4 = 14
In Dungeons and Dragons 5e, the authors actually assigned hit points to all the monsters that way. If a monster has 3d8 + 5 hit points, then they would use the following formula:
(8 + 1) / 2 × 3 + 5 = 18.5 (so 19 hit points, rounded up)
Try it a few times yourself! Roll 3d8, add 5, and see how close you are of 19. The likely hood is pretty high.
What do we get with character skill rolls?
Note that for rolling your statistics, you are allowed to roll 4d6 and pick the 3 that you prefer (in most cases, the 3 highest.) In that case, the odds are in your favor. Rolling 3d6 give you 1 / 63 chances to get an 18 (or a 3):
1 / 63 = 1 / 216 = 0.46%
When you roll 4 dice and discard one, you change your odds as follow:
To get 18, since you use the 3 largest dice, you have 3.5× more chances (there are 21 combinations of rolls with at least three 6 and you have to divide by 6 to normalize that number across all rolls). In other words:
1 / 63 x 21 / 6 = 1 / 64 * 21 = 1.62%
To get a 3, though, you divide by 6 since you are not going to use a 1 if any one die is not also a 1. So you have:
1 / 63 / 6 = 1 / 64 = 1 / 1296 = 0.0772%
That way all the numbers have a different odd to come up... This is shown in the following graph. The number 13 is the most likely to happen with 13.27% chance over all other numbers although 12, 14, 11, and 15 are not far behind. Just these 5 numbers have 60% to happen. The other 11 numbers share the other 40%.
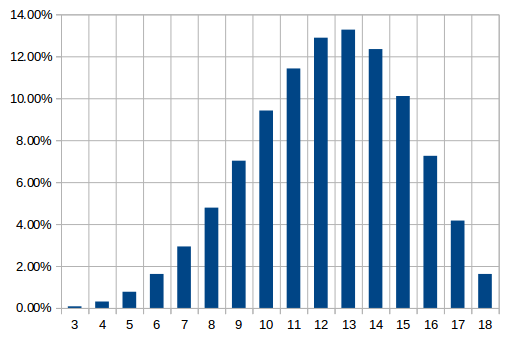
You will also notice that you have a much greater chance to get a larger number (15, 16, 17 and even 18) rather than a really low number (3, 4, 5). This makes it more fun because a character with really low statistics is not going to survive for very long.
How does that work with Advantage and Disadvantage in 5e?
In D&D 5e, you have the Advantage and Disadvantage rolls. For a normal attack, you roll a 1d20. Each number represents 5% chance. So if you need 14 or more to hit, you have (20 - 14 + 1) × 5% = 7 × 5% = 35% chance of hitting.
When rolling two dice with advantage and thus using the largest, you increase your chances to get a large number.
When rolling two dice with disadvantage and thus using the smallest, you increase your chances to get a smaller number.
The percent chances are shown below:
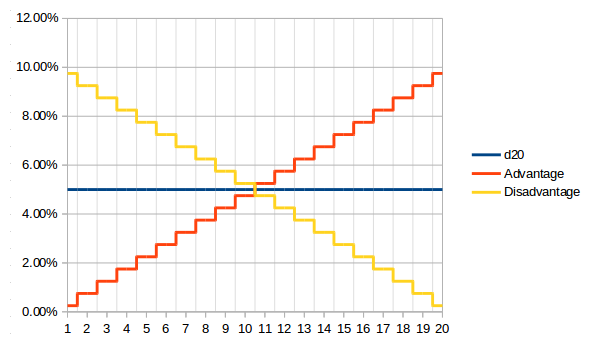
As we can see, this one is less intuitive. It is actually linear. It increases by 0.5% per number for advantage (Yes! You have 9.75% chance of rolling a 20 when having advantage! ... and 9.75% chance of rolling a 1 when having disadvantage!!!)
When just rolling 1d20 (the blue line), each number gets the exact same chance of 5%.
For our example of rolling a 14 or more with Advantage, you cumulate all the percentages from 14 to 20 and we get 57.75%. An extra 22.75% over a single die roll.
Wait, I just rolled a 1d4, how do I read the result?
Ah... So you noticed. The face of the die you need to read is on the table... and you cannot see through, right?
What you do is read the number written up straight at the bottom of the die.
There are a few d4 dice that have the number at the top instead. That's very similar, only if you don't expect it, it may take you a second before being able to reading the roll...

I thought D&D had a 1d100?
Indeed, some tables require the roll of a 1d100. A one hundred sided dice does not exist, though. Thus, what we do is roll two 1d10 and view one of them as the unit and the other as the tenth.
Many dice set actually come with 1d10 dices that have a zero behind the first digit (i.e. 00, 10, 20, 30, 40, 50, 60, 70, 80, 90). That way you can just add that die and the normal 1d10 die and you get a percent from 00% to 99% (most often the 00% is viewed as 100%.) This method has been in place for a while now, in part to make sure that the player is not going to choose which die represent which digit after they rolled.
The chance of getting any one specific number in this case is exactly 1%. This makes it easy to build a 1d100 table with increased or decreased chances of a certain number coming out.
I have seen people using 1d3 or 1d5, where are those dice?
Just like the 1d100, we use existing dice and change how we roll. For 1d3, we roll a 1d6 and read the result as follow:
| 1d6 | 1d3 |
|---|---|
| 1 or 2 | 1 |
| 3 or 4 | 2 |
| 5 or 6 | 3 |
You could also use some math. Roll a 1d6, divide by 2, round the result up.
Similarly, for a 1d5, we use a 1d10 and divide by 2.
In D&D 5e they changed that and instead spelled out the use of a dice. For example, instead of saying that a dragon will use its breath when rolling a 3 on a 1d3, they tell you roll a 1d6 and on a 5 or 6, the dragon uses its breath weapon. The result is the same, of course, but probably easier to understand.
What about some odd balls like a 1d7?
Well... first ask yourself, do we really need such a die?
But in many cases, yes, you can reach such a result.
For a 1d7, roll a 1d8 and if you get 8, re-roll until you don't get an 8.
Similarly for a 1d11, roll a 1d12 and if you get 12, re-roll until you do not get 12.
Really, this is making it complicated and probably won't add much to the game. Although I understand that once in while it can be useful. For example, with 11 characters and one of them has to do something specific and the players wanted to roll the die for it instead of one of them to move forward...
Isn't there a complicated name for the shape of each die?
Yes. There is a mathematical (a.k.a. Greek) name to each shape of the Dungeons & Dragons dice.
To be noted, all the dice have a convex shape. This makes sense since a concave shape would have faces on which the die could not land.
The Tetrahedron (d4)
The 4-sided die is a tetrahedron.
It is built from four equilateral triangles (all three sides of the triangles have the same length).
This is the only polyhedral shape with less than five faces.
Notice that it has four corners. The same number as its number of faces.
The word "Tetra-" comes from Greek (Tettares, Tessares) which means four.
The word "-hedron" is also a Greek word meaning the face of a geometrical shape.
So Tetrahedron means four faces in Greek.
The Cube (d6)
I would imagine that you are quite familiar with the Cube shape, composed of six squares and eight corners.
This is the shape most people think about when you speak of dice for playing a game. Most table board games make use of 6-sided dice.
The Octahedron (d8)
The 8-sided die is a regular Octahedron. Note that it is not composed of two Tetrahedra. Instead, it is two pyramids (bipyramid) glued together where all the edges have the same length.
Notice how the resulting shape faces all are equilateral triangles.
The Pentagonal Trapezohedron (d10)
The 10-sided die is composed of 10 faces which shape is called a kite. The die has a sharp corner between the 5 top faces and the 5 bottom shapes. The other corners are blunt.
In other words, this die is not quite regular even if all the faces have the exact same shape.
Dungeons & Dragons 10-sided dies are numbered from zero to nine (0-9) instead of one to ten (1-10). This is used to roll the 1d100 and thus in general makes more sense.
This is the one die which is not a Platonic Solid.
The Dodecahedron (d12)
The 12-sided die is composed of 12 regular hexagons. This is probably one of my favorite die. It really rolls nicely but not as long as a d20 (which at times ends up on the floor...)
There is always exactly three faces that meet at each vertex.
The oldest known Dodecahedron is Egyptian from 300 BC.
The shape is also found in nature where certain quasicrystals take the shape of a dodecahedron.
Fun Fact: the sum of the numbers on opposite sides is usually setup to equal 13.
The Icosahedron (d20)
The 20-sided die is an icosahedron. Icosa ("eíkosi") means 20 in Greek. Just like the Tetrahedron and the Octahedron, all the faces of an Icosahedron are equilateral triangles.
When Wizards of the Coast introduced Version 3e of Dungeons and Dragons, they made many changes, one of which was the heavy use of the d20 for all things D&D. As such, that version got the alias: « the D&D d20 version ».
In older versions of Dungeons & Dragons, the d20 was numbered 0 to 9, twice. In other words, they were using the d20 as a d10. This is because before Role Playing Games, people had Wargames which made use of percentages to determine success or failure of a hit. A d20 is still working like a d100, only the precision is cut down to make things easier. Note that you can still use a d20 as if it were a d10. Just ignore the tenth digit (i.e. the roll modulo 10—oh, sorry! Math again... ![]() ) and you get the same results as an old d20 by TSR.
) and you get the same results as an old d20 by TSR.
Why haven't we added more dice since D&D started in 1974?
What other die could you add? Ah... Good question, hum?
Well... I hope the statistics up there did not yet kill you... this is another mathematical problem. There are no other 3D shapes that form a regular die than the 1d4, 1d6, 1d8, 1d12, and 1d20 as was available in the very first Dungeons and Dragons.
These five shapes are called the Platonic Solids. It is called after Plato who actually proved way back then that there was only five such shapes. Yes, this means it was proven around 369 BC when Plato write his Theaetetus dialog. So this is human knowledge of more than 2,000 years.
So even if we wanted to introduce another die, it would not be possible. Although the 10-sided die is regular enough to work well, it's shape is not a platonic solid.
There was an attempt at creating a 1d100 (zocchihedron) for which a patent was written in 1985, but these do not work well. They tend to not stop rolling because each face is too small! It is nearly like a ping-pong ball. Not only that, unless you get a really big one, it is hard to read since the numbers have to be pretty small (100 numbers on such a small object...)
There are some other dice too. For example, Skull Splitter offers a 60-sided die as you can see on Amazon.com. Just like the 1d100 die, I do not recommend such because it is going to roll quite a bit before it stops and that's just not possible on a table with a map, 100 books, 100 other die, a master screen, miniatures, coffee, crackers...
Other sets I've seen include 1d3, 1d24, 1d30, 1d50 dice.
Where these dice invented by the authors of Dungeons & Dragons?
The dice themselves were certainly created by them (outside of the 6-sided die, obviously) for their game, but the shapes were all known before then.
The oldest objects that were used as dice where 1d4, pyramid like shapes. These appear around 3000 BC in what is now Turkey.
Before that, around 3100 BC, the Egyptians used two sided coin like objects to play the Senet game. Although personally I don't see those as dice, it was their way to introduce a certain amount of randomness in the Senet game.
The oldest d20 we found was buried in Egypt. It was used around 300 BC.
The Egyptians, again, had a d12 around 150 BC.
The 8-sided dice appear in 1888. It was called the poker die.
In 1906, someone patented the 10-sided die.
Again, a patent was written in 1950 for the d20 numbered 0 to 9 (twice). Actually, the first d20 used by TSR was also numbered from 0 to 9.




